Hydrostatischer Druck: Wie man ihn mit SOLIDWORKS Simulation modelliert

In einem mit Wasser gefüllten Tank zum Beispiel ist der hydrostatische Druck, den die Flüssigkeit auf die Tankwände ausübt, nicht konstant. Er ändert sich vielmehr mit der Höhe der Wassersäule.

Dies ist ein Tutorial für SOLIDWORKS SIMULATION.

Der hydrostatische Druck in SOLIDWORKS Simulation

Zunächst sollten Sie wissen, dass der hydrostatische Druck in der folgenden Form ausgedrückt wird: P = ρgh

• P: Druck (in N/m2).

• ρ : Dichte der Flüssigkeit (in Kg/m3): 1000 Kg/m3 für Wasser.

• g: Erdbeschleunigung (in m/s2 oder N/Kg): 9,81 m/s2

• h: Tiefe oder Höhe der Flüssigkeitssäule (in m).

Für Wasser gilt also P = 1000 * 9,81 * h = 9810 * h.

Bei einer Wassertiefe von 10 m ergibt sich also tatsächlich ein Druck von 1 bar (100000 N/m2).

In SOLIDWORKS Simulation hat man die Möglichkeit, variable Verteilungen von Kräften oder Drücken zu verwenden. Dazu muss man sie in einem XY-Koordinatensystem in folgender Form ausdrücken: P(x,y) = P(a+bX+cY+dXY+eX2+fY2). Übrigens wird das XY-Koordinatensystem über ein "Koordinatensystem" definiert.

Anwendungsbeispiel zur Modellierung des hydrostatischen Drucks.

Im folgenden Beispiel habe ich ein Viertel eines Tanks gezeichnet. Mithilfe einer Trennlinie wird der Wasserstand im Tank materialisiert. Ein "Koordinatensystem" wurde erstellt, dessen Ursprung auf der Trennlinie liegt und dessen Y-Achse zum Boden des Tanks hin ausgerichtet ist. Dann fügte ich eine ebene Auflage am Boden des Tanks, eine Einbettung am unteren Ende der Versteifung und die Symmetriebedingungen für die Berechnung hinzu.

Um dann den variablen Druck auf die Wände des Tanks anzuwenden, müssen Sie, nachdem Sie die Flächen ausgewählt haben, die Option "Variable Verteilung" verwenden. Am einfachsten ist es, den Druckwert auf 1 zu setzen. Tatsächlich stellt dieser Wert im Fall einer variablen Verteilung den Multiplikator P dar, der in der zuvor gesehenen Gleichung erscheint. Dann geben Sie einfach den Koeffizienten für Y ein und lassen alle anderen auf 0 stehen. In unserem Beispiel steht Y für die Höhe der Wassersäule, die zwischen 0 und 2,3 m variiert.

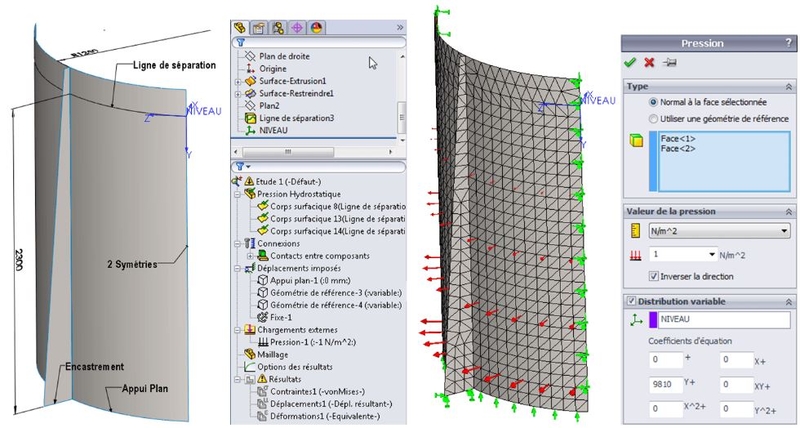
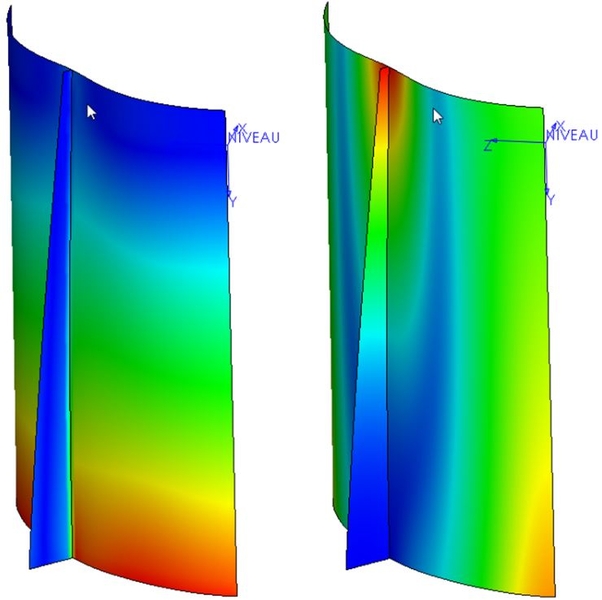
So können Sie nach der Validierung des Drucks feststellen, dass die Größe der Drucksymbole mit zunehmender Tiefe des Behälters zunimmt. Im Folgenden werden Ergebnisse in Bezug auf Spannung und Verschiebung dargestellt.