Hydrostatic pressure: how to model it with SOLIDWORKS Simulation

In a tank filled with water, for example, the hydrostatic pressure exerted by the liquid on the tank walls is not constant. In fact, it varies with the height of the water column.

This is a tutorial for SOLIDWORKS SIMULATION.

Hydrostatic pressure in SOLIDWORKS simulation

First of all, hydrostatic pressure is expressed as: P = ρgh

• P: Pressure (in N/m2)

• ρ : density of the liquid (in Kg/m3): 1000 Kg/m3 for water

• g : acceleration of gravity (in m/s2 or N/Kg): 9.81 m/s2

• h: Depth or height of liquid column (in m)

So, for water P = 1000 * 9.81 * h = 9810 * h

So, for a water depth of 10 m, the pressure is 1 bar (100,000 N/m2).

In SOLIDWORKS Simulation, you can use variable force or pressure distributions. To do so, they must be expressed in an XY frame of reference in the form: P(x,y) = P(a+bX+cY+dXY+eX2+fY2). Incidentally, the XY reference frame is defined by a "coordinate system".

Example of use to model hydrostatic pressure

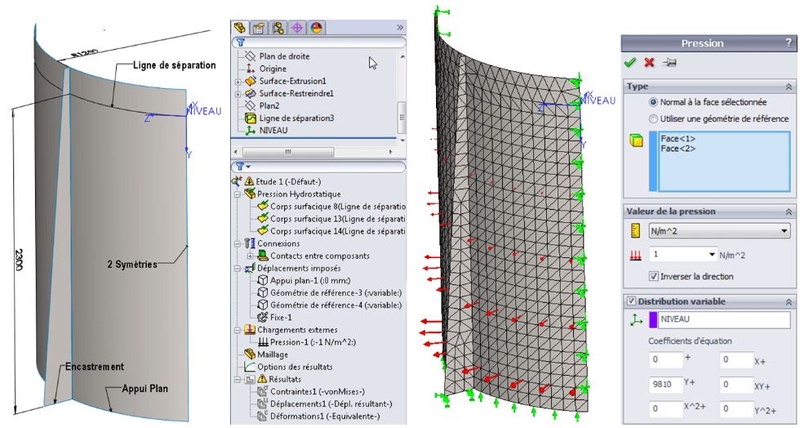
In the example below, I've drawn a quarter tank. A dividing line materializes the water level in the tank. A "Coordinate system" has been created, with its origin on the dividing line and the Y axis oriented towards the bottom of the tank. Next, I added a flat support at the bottom of the tank, a recess at the bottom of the stiffener and the symmetry conditions for the calculation.

Then, to apply the variable pressure to the tank walls, once the faces have been selected, you need to use the "Variable Distribution" option. The easiest way to do this is to set the pressure value to 1. In fact, in the case of variable distribution, this value represents the multiplication coefficient P which appears in the equation seen previously. Next, simply enter the Y coefficient and leave all others at 0. In our example, Y represents the height of the water column, which varies from 0 to 2.3m.

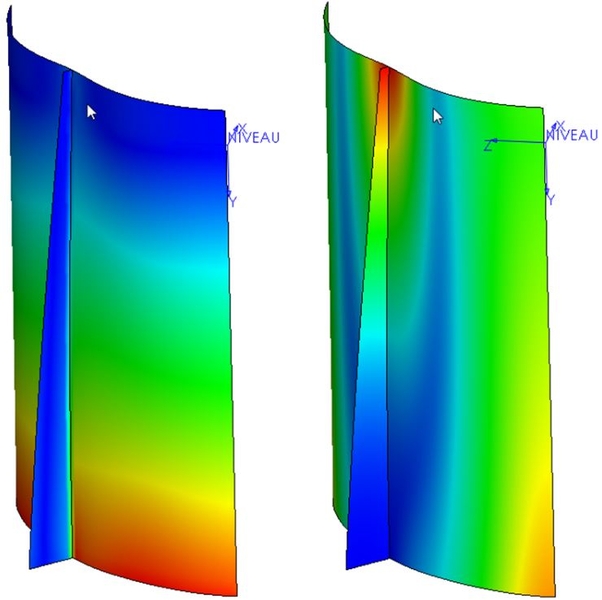
So, once the pressure has been validated, you can see that the size of the pressure symbols increases with the depth of the vessel. Here are the results in terms of stress and displacement.